|
|
Home > Problems > Chapter 5
| To locate Web sites of programs specified in the problems, perform a Web search using the program name. Instructors may also wish to set up local copies of these programs, which is best done on a UNIX or Linux server.
|
1. Practice using the CLUSTALW program to align the set of proteins in the RAD51-RECA group. These proteins all promote homologous DNA strand interactions during genetic recombination between DNA molecules. The sequences may be retrieved from the SwissProt server (perform Web search to find link to SwissProt) by their accession numbers in FASTA format: P25454, P25453, P03017, P48295. Use a simple text editor to make a FASTA multiple sequence by catenating these individual sequence files into one FASTA msa file (see p. 53).
- Locate a CLUSTALW Web site. This program is available for PCs and also on a Web site at Baylor College of Medicine (BCM) searchlauncher site.
- Copy and paste the catenated FASTA sequence file into the CLUSTALW data window.
- Use the default alignment conditions provided by the program.
- Note the two kinds of msa output formats. One is the align format with numbers, and the second is the FASTA format with the aligned sequences joined end to end in FASTA format, with gaps in each sequence corresponding to the alignment.
- Save this file for later reference.
|
2. Go to the BAliBASE Web site and retrieve the SwissProt accession numbers of the 1csy (SH2) group of proteins that align in the 20-40% identity, reference 1 range.
- Retrieve these sequences from SwissProt and, using a simple text editor, place them in the FASTA msa format. Note that the BAliBASE alignments are based on known structural alignments and therefore are a test of the ability of msa programs to provide an msa that is structurally correct.
- Try to align these proteins by searching for the POA, DIALIGN, and CLUSTALW Web sites and pasting the sequences into the program sequence window.
- Compare the alignments to the correct ones on the BAliBASE site and note which program, if any, does the best job.
|
3. When a global msa can be made, one can pick out the most conserved regions (motifs), make a scoring matrix, and search for other sequences that have this same motif. The matrix will take into account the variation found in the sequences. We will make a position-specific scoring matrix (PSSM, also called a scoring matrix, or weight matrix) by hand corresponding to a short msa and then use the matrix to scan a sequence. Here is a table showing the frequency of each base in an alignment that is four bases long:

- Assuming that the background frequency is 0.25 for each base, calculate a log odds score for each table position; i.e., log to the base 2 of the ratio of each observed value to the expected frequency.
- Align the matrix with each position in the sequence TGAGCTAA starting at position 1, 2, etc., and calculate the log odds score for the matrix to match that position.
- Now convert the alignment scores to ODDS scores, sum them, and calculate the probability of the best matching position.
|
| 4. In question 3, we assumed that we already have a global alignment of a set of sequences so that a scoring matrix could be made from the alignment. Although we may know that a set of sequences has the same function, and thus should align, the sequences may vary so much that it is difficult to align them globally. In this case, we have to resort to a statistical analysis to find conserved patterns. The following problem goes through the first few steps required to find the best alignment by a statistical method. Students will need to study first the example of the expectation maximization algorithm in the text.
Analyze the following ten DNA sequences by the expectation maximization algorithm. Assume that the background base frequencies are each 0.25 and that the middle three positions are a motif. The size of the motif is a guess that is based on a molecular model. The alignment of the sequences is also a guess.
seq1 C CAG A
seq2 G TTA A
seq3 G TAC C
seq4 T TAT T
seq5 C AGA T
seq6 T TTT G
seq7 A TAC T
seq8 C TAT G
seq9 A GCT C
seq10 G TAG A
- To start the PSSM, make a table with three columns (position in motif) and four rows (1 for each base).
- Calculate the observed frequency of each base at each of the three middle positions in the alignment.
- Using the frequencies in the column tables, and the background frequencies, calculate the odds likelihood of finding the motif at each of the possible locations in sequence 5.
- Calculate the probability of finding the motif at each position in sequence 5.
- Calculate what change will be made to the base count in each column of the motif table as a result of matching the motif to the first position in sequence 5. This is usually a fractional number of one base.
- What other steps are taken to update or maximize the table values?
|
5. MEME is a server that will take as input a set of sequences and find alignment by the expectation maximization method.
- Paste the same unaligned RAD51-RECA sequences (problem 1) into the sequence window and use the defaults provided by the program. Students will need to provide their own E-mail address to receive results.
- Examine the results and note how many conserved regions were found.
- Save these results for later analysis.
|
6. A simplified hidden Markov Model (HMM) is shown below. (Red square, match state; green diamond, insert state; blue circle, delete state—probability of 1; arrows, probability of going from one state to the next.)
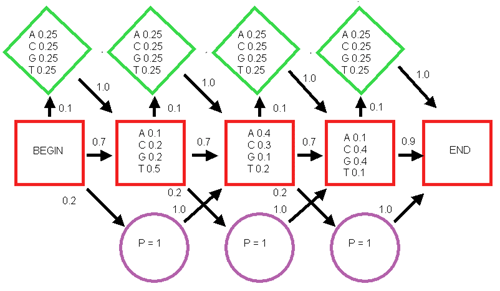
- Calculate the probability of the sequence TAG by following a path through the model starting at Begin, going through each of the three match states (red squares), and ending at End.
- Repeat step a for a path that, starting at Begin, goes first to the first insert state (green diamond), then to a match state (red square), then to a delete state (blue circle, probability 1 for any character in this state), then to a match state, and finishes at End.
- Which of the two paths is the more probable one, and what is the ratio of the probability of the higher to the lower one? The highest-scoring path is the best alignment of the sequence with the model.
- To improve the model, we keep adjusting the scores for the states and transition probabilities by aligning additional sequences with the model using an HMM adaptation of the expectation maximization algorithm. In the expectation step, we calculate all of the possible paths through the model, sum the scores, and then calculate the probability of each path. Each state and transition probability is then updated by the maximization step of the algorithm to make the model better predict the new sequence.
For this example, suppose that the model has been made from 30 sequences, and that the alignment of TAG in step a has a probability of 1.0; i.e., this path is overwhelmingly the best of all possible paths through the model. What would be the new fractions in the first match state? (Note that only a fraction of the sequences originally passed through the first state�think carefully about how many actually did.) Similarly, what would be the new values for the transition probabilities from Begin to this first match state, assuming that 0.7 of the 30 sequences followed the path from Begin to the first match state? (Hint: Updating the match state frequencies should be done by going back to the raw base numbers in each column. Similarly, updating the transition probability should be done by counting the number of sequences that would have followed the path from Begin to the first match state.)
- Change all the values in each of the states to log odds scores, assuming that the frequency of each base is 0.25. Also change the transition probabilities to log odds, i.e., log to base 2 of the ratio of observed transition probability to background probability. (Note: Transition background is an equal probability of making a transition to each subsequent state and will be calculated by dividing 1 by the number of possible transitions from each state; i.e., the background probability will be one of 1/2 = 0.5, 1/3 = 0.33, or 1/1.) Now calculate the probability in step a as a log odds score.
|
7. Analyze the following ten DNA sequences by the Gibbs sampling algorithm.
seq1 C CAG A
seq2 G TTA A
seq3 G TAC C
seq4 T TAT T
seq5 C AGA T
seq6 T TTT G
seq7 A TAC T
seq8 C TAT G
seq9 A GCT C
seq10 G TAG A
- Assuming that the background base frequencies are 0.25, calculate a log odds matrix for the central three positions.
- Assuming that another sequence G TTT G is the left-out sequence, slide the log odds matrix along the left-out sequence and find the log odds score at each of three possible positions.
- Change each log odds score to an odds score and sum the odds scores. Calculate the probability of a match at each position in the left-out sequence. (Odds score = 2 raised to the power of the log odds score.)
- How do we choose a possible location for the motif in the left-out sequence?
|
8. This problem explores the information content of a scoring matrix by the relative entropy method (ignores background frequencies). Read the notes on information content of sequences on page 213 before trying this problem.

- Calculate the entropy or uncertainty (Hc) for each column and for the entire matrix.
- Calculate the decrease in uncertainty or amount of information (Rc) for column 1 due to these data (for DNA, Rc = 2 – Hc and for proteins, Rc = 4.32 – Hc).
- Calculate the amount that the uncertainty is reduced (or the amount of information contributed) for each base in column 1.
|
|
|
| © 2004 by Cold Spring Harbor Laboratory Press. All rights reserved. |
 |
| No part of these pages, either text or image, may be used for any purpose other than personal use. Therefore, reproduction, modification, storage in a retrieval system, or retransmission, in any form or by any means, electronic, mechanical, or otherwise, for reasons other than personal use, is strictly prohibited without prior written permission. |
|
|
|